Vyplňto.cz > Průzkumy > Archiv výsledků > Srovnání Hejného a klasické matematiky
Srovnání Hejného a klasické matematiky
→ Mohou Vaši podřízení pracovat z domova? Sledujete nějak, co v práci dělají a zda nedělají vedle práce ještě něco jiného? ←
(průzkum pro diplomovou práci, cca 10 minut)
Základní údaje o provedeném průzkumu
| Autor průzkumu: | Natália Šťastná |
|---|---|
| Šetření: | 07. 06. 2018 - 21. 06. 2018 |
| Počet respondentů: | 141 |
| Počet otázek (max/průměr): | 26 / 22.21 |
| Použité ochrany: | žádné |
| Zobrazení otázek: | po jedné otázce |
| Návratnost dotazníků: | 62,4 % |
| Návratnost dotazníků je dána poměrem vyplněných a zobrazených dotazníků. Jedná se o orientační údaj, který nebere v potaz ty oslovené respondenty, kteří ani nezobrazili úvodní text (neklikli na odkaz na dotazník). | |
| Průměrná doba vyplňování: | 00.04:47 |
| odpovědi & grafy segmentace závislosti zdroje dotazník citovat | |
Úvodní informace zveřejněné respondentům
Dobrý den,
jsem studentkou pedagogické fakulty a momentálně sbírám data pro svou diplomovou práci věnující se srovnání klasické a Hejného matematiky.
Dotazník obsahuje 26 otázek a je určen učitelům na prvním stupni základních škol. Zabere Vám max. 10 min. Budu velmi ráda, pokud se se mnou podělíte o svůj názor a zkušenosti s výukou matematiky.
Děkuji, Šťastná N.
Odpovědi respondentů
1. Jakou metodou vyučujete matematiku ve své třídě?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Kombinuji prvky z obou metod | 53 | 37,59 % | 37,59 % |
| Klasickou metodou | 51 | 36,17 % | 36,17 % |
| Hejného metodou | 37 | 26,24 % | 26,24 % |
2. Mohli jste si vybrat, jakou metodou budete matematiku vyučovat?
Povinná otázka, respondent se musel rozhodnout mezi odpověďmi „ano” a „ne”.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| ano | 94 | 66,67 % | 66,67 % |
| ne | 47 | 33,33 % | 33,33 % |
3. Měli jste možnost vyučovat klasickou metodou?
Povinná otázka, respondent se musel rozhodnout mezi odpověďmi „ano” a „ne”.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| ano | 125 | 88,65 % | 88,65 % |
| ne | 16 | 11,35 % | 11,35 % |
4. Měli jste možnost vyučovat Hejného metodou?
Povinná otázka, respondent se musel rozhodnout mezi odpověďmi „ano” a „ne”.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| ano | 103 | 73,05 % | 73,05 % |
| ne | 38 | 26,95 % | 26,95 % |
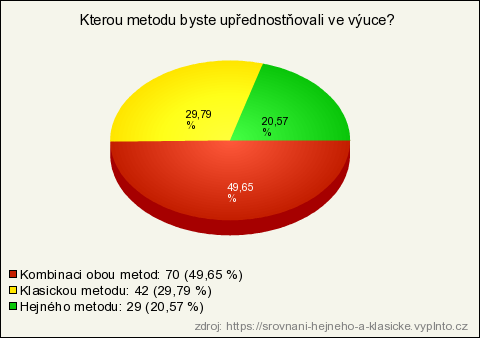
5. Kterou metodu byste upřednostňovali ve výuce?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Kombinaci obou metod | 70 | 49,65 % | 49,65 % |
| Klasickou metodu | 42 | 29,79 % | 29,79 % |
| Hejného metodu | 29 | 20,57 % | 20,57 % |
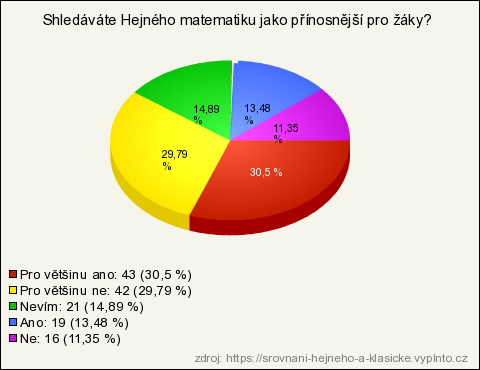
6. Shledáváte Hejného matematiku jako přínosnější pro žáky?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Pro většinu ano | 43 | 30,5 % | 30,5 % |
| Pro většinu ne | 42 | 29,79 % | 29,79 % |
| Nevím | 21 | 14,89 % | 14,89 % |
| Ano | 19 | 13,48 % | 13,48 % |
| Ne | 16 | 11,35 % | 11,35 % |
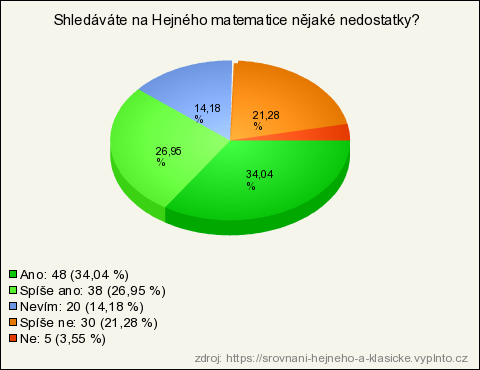
7. Shledáváte na Hejného matematice nějaké nedostatky?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Ano | 48 | 34,04 % | 34,04 % |
| Spíše ano | 38 | 26,95 % | 26,95 % |
| Spíše ne | 30 | 21,28 % | 21,28 % |
| Nevím | 20 | 14,18 % | 14,18 % |
| Ne | 5 | 3,55 % | 3,55 % |
8. Pokud ano, uveďte jaké:
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
- pokud se vše nechává- až si na to přijde samo-tak se může stát, že si na to prostě nepřijde včas!!!! A ve 4. třídě plave skoro ve všem, protože už od 2 vůbec nechápe řády desítek,jednotek……. (a ve čtvrté je potřeba toto i u římských číslic, u převodů, prostě všude) - jeden z příkladů
1 třída - chybí sčítání a odčítání přes desítku s přechodem - nebere se tam vůbec na to ohled.
C
d
děti jsou méně hbité v početních dovednostech
Existence
Hejného matematika je pro nadané žáky, kteří mají matematickou představivost. Ostatní se musí matematiku nadrilovat. Byla jsem na pár školeních, viděla videa a nikdy.
chybí porozumění a shoda mezi odborníky, neporozumění rodičů, nedostatečná podpora vedení školy, problém u dětí s určitými problémy- např. PAS- chybí představivost, nechce pořád něco "zkoušet", svět je pro něj nesrozumitelný, objevuje ho obtížně
chybí sloupečky příkladů k automatizaci
Je to nepraktické a zdlouhavé
Je to v podstatě vysokoškolský způsob výuky aplikovaný na problematiku matematiky základní školy a některé děti (ani jejich rodiče) na to nejsou zralé a mnohem snadněji se odrazí od "naservírované" klasické matematiky. V Hejného metodě se snadno ztratí a k jádru problému se ani nedostanou, natož aby ho nějak uchopily a pracovaly s ním dál.
Každá metoda má své nedostatky. Já upřímně v pomalejším tempu postupu. Nebo nutnosti informovat rodiče o typech úloh a řešení.
MALÁ ZNALOST POČTŮ, POMALOST, NE VŠICHNI ŽÁCI JSOU NUCENI AKTIVNĚ PACOVAT
Malo procvicovani
Málo prostoru k procvičování mechanického počítání - slabší děti zapomínají např. algoritmy písemného sčítání, odčítání, násobení, dělení.
Malý prostor - geometrie (rýsování, pojmy). Málo procvičování klasických příkladů, násobilkových spojů apod. Šikovní pracují, slabší se vezou...
Mám dojem, že děti vyučované Hejného metodou nemají tak zautomatizované početní spoje. Je fajn, že H. metoda učí děti logicky myslet a je hravá a zábavná, jenže ten, komu je logické uvažování tak trochu cizí, je v ní ztracen. Zaujímá pak sice ve výuce pozici pozorovatele, ale v praktickém životě je třeba umět i "obyčejně" počítat:-)
Mám zkušenost s 1. a 2. ročníkem. Moc barevná, odvádí pozornost žáků. Časté přeskakování z prostředí na prostředí - slabší žáci potřebují novinky v prostředí více procvičit.
Menší prostor pro numerické počítání, ale numerické počítání nepovažuji za nejdůležitější, ale rodičům někdy chybí.
mnoho
Množství variant pro menší děti nepochopitelné.
Myslím si, že Hejného metoda je pro chytřejší žáky, ve vyšších třídách mají ti průměrní problémy. Další velký problém je, že střední školy s Hejného metodou nejsou.
Na některé typy úloh slabší děti nemohou přijít bez nápovědy či prozrazení jak na to.
Naprosto nevhodné pro autisty, dyskalkuliky - vlastní praxe. Děvče nebylo schopné řešit logické úlohy. Ve skupinách pohodlné děti nepracují, jen se vezou. Nebaví se o řešení, ale o tom, co je "zajímá". No a propadlí , kteří měli Hejného a nezvládali počítat ani do 10, teď počítají s názorem v pohodě. Otázka je, co je klasická metoda, protože kupu prostředí znám z letité praxe a nechat děti najít své řešení a podělit se o ně s ostatními - to jde i bez Hejného metody.
Např. Zavedení sčítání s přechodem přes bez vysvětlení v 1. pololetí, někdy složitá zadání, takový pel mel bez pravidel.
násobilka
Násobilka
Násobilka se neučí zpaměti
Návaznost na druhý stupeň
Ne vsechny deti jsiu schopne ukoly zvladat
nedostatečné upevnění učiva, hlavně pro žáky s krátkodobou pamětí, nedostatek procvičovacích svičení, přeskakování z jednoho učiva do druhého, občasná nesrozumitelnost zadání (Kdybych neměla příručku učitele s výsledky, občas opravdu nevím, jak to myslí, nehledě na to,ž e je tam velká spousta chyb ve výsledcích)
Nedostatek cvičení k zautomatizování matematických operací, zvláště násobení, dělení, písemného odčítání a písemného násobení.
Nejsem si jistá, zda je vhodná pro výuku matematiky v málotřídní škole, kde jsou třeba tři ročníky v jedné třídě.
Někteří žáci nezvládájí ani nejlehčí úkoly.
nenavazuje ve vyšších ročnících na systém klasické výuky
Není pro všechny žáky. Chytřejší si s ní poradí lehce, pomalejší v ní plavou a nejsou schopni se dopátrat výsledků.
Není pro všechny, práce s chybou
Není to metoda vhodná pro všechny děti ve třídě. Některé děti vůbec netuší, co mají dělat a nejsou schopné některá prostředí plně pochopit. V Hejného matematice je nedostatek pamětného počítání, procvičování, samostatné práce a rýsování.
Není vhodná pro děti s LMP, je založena na dynamickém myšlení. To tyhle děti nemají.
není vhodná pro děti, kterým chybí logické myšlení
Neumí klasickou matematiku, potřebuji stále názor.
neupevněná násobilka, chybí pamětné počítání
Nevhodná pro žáky se SVP
Nevyvozuji se základní početní operace, tento systém nevyhovuje slabším žákům
neznalost násobilky, pamětného počítání, rýsování
Nutnost doplnění výuky o pamětné počítání.
Od čtvrté třídy se děti v úkolech ztrácení, jsou pro ně náročné a raději počkají, až na řešení přijde někdo jiný.
Osvědčuje se pro bystré žáky, nevede k osvojení numerického počítání. Kdo nemá logické myšlení, stejně ho nezíská.
pokud by se třída věnovala jen Hejného mat., pak nemají upevněné procvičování numerace, násobilky
Pomale
Poznámky o tom, že se žáci nemají násobilku učit zpaměti,..
Pro děti s SPU jsou některé úkoly velice obtížné, pro děti s mentální retardací naprosto nepochopitelné, a v rámci inkluze je potom těžké spojit vše dohromady.
Pro méně Intel děti obtížné, pro rodiče též.
Pro slabší žáky je příliš obtížná. Nedokáží prostředí pochopit.
Protože ji kombinuji, tak bych uvítala v Hejného matematice více početních příkladů, pozvolnější tempo, méně prostředí.
Přemrštěné učebnice, problém s hodnocením, nutno komunikovat s rodiči, aby matematiku nezavrhli, když ji nerozumí.
rodiče a kolegové ji nerozumí,není možnost pokračování na jiné škole
Rychlé pamětné počítání je velmi slabé, slabé děti se v úlohách necítí, rodiče nevědí, co s úkoly.
Rychlost
Tak nedostatkem je, že tento způsob není úplně pro všechny, hlavně ne pro rodiče a konzervativní jedince z řad učitelstva....
V 1.-3. ročníku přeskakování z prostředí na prostředí, málo procvičování nově zavedených prostředí, ve 4.-5. ročníku některé učivo příliš do hloubky, některé nedostatečné (např. převody jednotek, geometrie)
V nekterych pripadech je potrebna dynamika kolektivu, kterou napriklad doma vzdelavajici rodice nemaji moznost zajistit.
více klasických příkladů na počítání - pro rodiče
vše
vše
vše, nelze je nechat, aby si přišli na řešení
všechno
všechny, není to pro slabé děti
založeno na logickém myšlení, slabší žáci se k výsledku těžko dopracují; názor je nadužívám i ve chvíli, kdy ho není potřeba
Ze zkušeností z praxe: těžší na pochopení u některých slabších dětí, složité úkony-ne každý to chápe.
Žáci nemají jistotu, že vypočítali příklad správně, nejsou si jistí v běžných početních operacích, mají velké problémy s rýsováním.
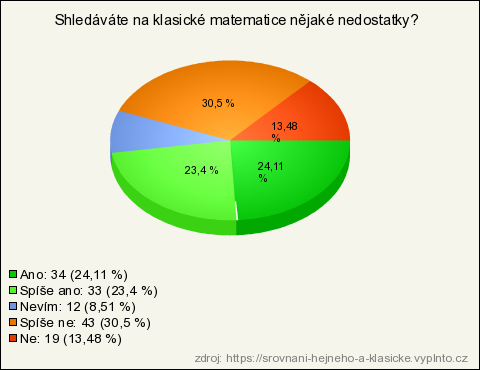
9. Shledáváte na klasické matematice nějaké nedostatky?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Spíše ne | 43 | 30,5 % | 30,5 % |
| Ano | 34 | 24,11 % | 24,11 % |
| Spíše ano | 33 | 23,4 % | 23,4 % |
| Ne | 19 | 13,48 % | 13,48 % |
| Nevím | 12 | 8,51 % | 8,51 % |
10. Pokud ano, uveďte jaké:
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
- málo atraktivní, nudné, málo podnětné, zbytečný důraz na rychlost,....
- nedostatečný rozvoj prostorové orientace - malý rozvoj logického myšlení - dítě se zde nesetkává s úlohami, které nemají řešení nebo mají více řešení - neučí je kritickému myšlení, zamýšlení se nad úlohou/problémem
a
absence gradovaných úloh, absence úloh podporujících logické myšlení, většina výuky založena na ovládání algoritmů
Dril
dril
Dril bez pochopení.Stale stejně příklady.Nuda.
dril, malá variabilita úloh
hravost, nápaditost, netrtadiční úlohy, práce s chybou, úlohy, které nemají řešení
Je nudně postavená. Pokud si ucitel sám nevymýšlí nebo nedohledává aktivity k rozvoje logického myšlení, je odkázán na nudnou metodiku klasiky. Vždy jsem zaváděda obdobné prvky, které používá H mat.
Je nutné docela často používat formulaci "teď se tím nebudeme zabývat, budeme se to učit později", na některé souvislosti je potřeba upozorňovat a žákům na ně s důrazem poukazovat, je potřeba děti více motivovat, proč se co vlastně učí když to vypadá tak " nepoužitelně"
Je příliš memorovací, nevede k hlubšímu pochopení.
Je v ní méně hravých a tvořivých prvků, pokud se o jejich začlenění učitel vysloveně nesnaží. Do určité míry lze např. početní spoje nabiflovat. Zpravidla většinu dětí tolik nebaví.
Jen počítání bez logiky.
Klasická matematika je taková, jakou si ji učitel ve třídě udělá. Může být plná her a soutěží, aktivit na spolupráci nebo samostatné činnosti. "Klasická matematika" není metoda jako taková. "Frontálka" je samozřejmě špatná, vede k nudě učitele i dětí. Ale frontálku snad dnes už neučí žádný kompetentní pedagog.
Klasická matematika tolik nepodnecuje děti k vlastnímu uvažování, nemají tolik potřebu nad úlohou přemýšlet, zkoušet různé způsoby řešení apod. Nerozvíjí se tolik jejich matematické myšlení.
málo logického uvažování
Málo logických úloh
Málo logiky, rozvoje představivosti atd.
Málo procvičování logického uvažování
Málo z praxe, hodně teorie, pametneho učení.
Mechanicke uceni, spoustu deti nepochopi zaklad a nikoho nezajima ze jim to nejde
Memorování
Méně rozvíjí logické myšlení. Nebaví děti tolik jako HM.
Motivaci, nudu, nízká možnost objevování
Možná menší rozvoj logického myšlení, ale to si dobrý učitel do hodin zapojí sám.
Ne každému dítěti vyhovuje takový postup práce. Příliš frontální.
Nedostatečné rozvíjení kreativity.
nedostatek kreativity, samostatného objevování
Nechuť dětí přemýšlet, hledat řešení. Jsou to po čase jen sčítači sloupečků.
Někdy méně nápaditá, moc příkladů ve cvičeních
Některé příklady jsou pro žáky málo atraktivní, v učebnicích úlohy běžně nebývají gradované. Pro nadané žáky bývá málo problémových příkladů.
není vhodná pro všechny
Nenutí děti tolik přemýšlet.
Nepodnětná cvičení, která nerozvíjejí logiku, kombinatoriku a málo příležitostí k objevování.
Nerozvíjí logické myšlení, schopnost argumentovat, nedává prostor pro vlastní řešení, předkládá dětem postupy, nerozvíjí spolupráci a nepomaha dítěti rozvíjet jeho osobnost
Nerozvíjí u dětí logické myšlení, neučí je jak efektivně řešit problémy
Nezazivnost uciva, mala aktivita zaku
NUDA
postupy jsou jasně dané, děti pak méně přemýšlí
Předkládá žákům hotové postupy, málo se v ní objevuje, důraz je kladen na dril, méně na hledání jiných postupů.
předkládá žákům jeden způsob řešení, nepodporuje tolik kreativitu a samostatné myšlení
přednost formy před obsahem (slovní úlohy - zápis), nedostatečné budování matematických představ, logického uvažování,
příliš velký důraz na dril, děti nebaví a nezajímá, nenechává prostor pro vlastní objevy, neposkytuje tolik prostoru pro diferenciaci, počítá s tím, že teď hned všichni se naučí danou látku (není to až tak ale chyba matematiky, ale části učitelů a prac. sešitů, které k tomu svádí)
Přímo mi vadí, že se např. dětem zatajuje, že lze počítat např. 4-5. Učila jsem klasickou metodou vlastně celý život a žádný příklad a na odčítání většího čísla od menšího v učebnicích nebyl. Děti ale záporná čísla z praxe znají( teploměr).
rozvoj logiky a prostorové představivosti
Rutinní, jednotvárné úkoly zaměřené na příklady, u kterých není potřeba přemýšlet.
Rychlost
Stereotyp,nerozvíjí logické myšlení,pro žáky nudná.
Stereotypní úlohy, důraz na rychlost
U některých učitelů tempo při nácviku nového
Učení na základě paměti, učení bez pochopení.
V
Zajímavé typy úloh
Založení na memorování, bez vytvoření myšlenkových map či logických postupů.
Zbytecne memorovani Chybí pochopen Nazornost Tvorivost
Zbytecne opakovani, pomaly postup, vysvetlovani nove latky bez prozitku, mala rozmanitost uloh
Zvídavější děti se nudí.
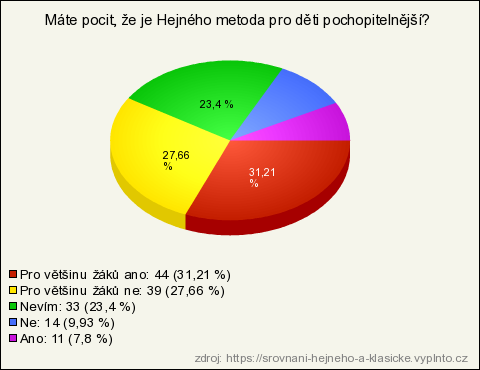
11. Máte pocit, že je Hejného metoda pro děti pochopitelnější?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Pro většinu žáků ano | 44 | 31,21 % | 31,21 % |
| Pro většinu žáků ne | 39 | 27,66 % | 27,66 % |
| Nevím | 33 | 23,4 % | 23,4 % |
| Ne | 14 | 9,93 % | 9,93 % |
| Ano | 11 | 7,8 % | 7,8 % |
12. Prosím, uveďte, co je pro děti pochopitelnější.
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
-je to hravější a tím to děti více zajímá -tím lépe chápou
?
a
B
ČÁST POTŘEBUJE POMOCI K ÚPOCHOPENÍ UKÁZKU POSTUPU. NE VŠICHNI UMÍ OBHJEVIT CESTU A USPĚT - PTŘEBUJÍ PRŮVODCE V PRVNÍCH KROCÍCH
děti lépe pochopí systém násobení, zlomků apod.
Děti mají pocit, že si hrají, řeší hádanky, rébusy. Prostředí se vysvětlují přes vlastní zkušenost např. krokování. Žáci vysvětlují žákům dětským, více pochopitelným jazykem.
Děti nezvládají Dědu lesoně - dle dětí"nesmyslné přepočty". Otázka chlapce, který má průměr 1.00 : "Paní učitelko, budu to v životě potřebovat?" já: "Asi ne". dítě: "Tak proč ten nesmysl musíme počítat?" Totéž u indického násobení. Dítě není schopno nakreslit tabulku, aby do ní počítalo.
děti už většinou mají ve školky vybudovanou představu o čísle, proto mně přijde v podstatě jako zdržování sčítání pomocí čárek
Formou hry dokáží hravě přijít, vyřešit velmi složité úlohy (které se mnohdy probírají až na druhém stupni)
Hejného
chápání abstraktních pojmů
Jak co, jak pro které děti...některé vůbec nechápou autobusy (u Hejného), někteří se díky nim krásně naučí představivost. Dále třeab klasické písemné násobení již často diskutabilní "Podržím si 1/2/...", které přičítám k dalším řádům je nepochopitelné pro spousty žáků, u Indického násobení u Hejného je krásně vidět kam se ta čísla vpisují a proč.
Jasně zadané postupy
je intuitivnější.
Je přirozenější, kopíruje vývoj mozku.
každému sedne jiné prostředí. Moji žáci např. milují násob.obdélníky, přitom se násobilku naučili zpaměti. Naopak nenávidí prostředí -autobusu 2
Klasická matematika doplněná o příklady z praxe a různé zajímavé hříčky
klasická metoda
Klasická metoda
Klasická metoda.
klasika, která pomáhá těm slabším a dává jim kuchařku, jak na to
Krokovací pás je bezva věc.
Logické myšlení
Mají lepší představu čísla, matematické operace nejsou pouhou abstraktní položkou. Zvyšuje se jejich prostorová představivost.
Mají možnost si věci osahat a namodelovat, jsou vedené k přemýšlení v souvislostech, neučí se jednotlivé jevy izolovane
možnost si vše vyzkoušet, ohmatat a chyba není chyba, ale možnost jak se dopátrat správného výsledku
Možnost spolupráce,
Možnost zpětně vazby- ověření v praxi
Myslím, že v začátcích je pochopitelnější, hlavně pro to, že se nejprve používají čárky a obrázky místo číslic. Počítání v matematických prostředích je ale pro některé žáky mnohem náročnější než "klasické" počítání. Záleží na konkrétním žákovi ;-).
Na podstatu věci si přijdou sami a lépe ji porozumí a více si toho zapamatují, tím, že si to prožijí
Na spoustu věcí přicházejí různými způsoby, mají možnost diskutovat a tím lépe chápat vztahy.
Např. již v 1. třídě lépe pochopí díky krokování princip sčítání a odčítání a to i v prostředí záporných čísel....
Např. úlohy na výpočet obsahu a obvodu rovinných obrazců, povrchu krychle, úlohy s e zápornými čísly - děti si je při použití Hejného metody doslova ohmatají, zažijí. Nebo rovnice pomocí prostředí zvířátek dědy Lesoně.
názornost
názornost
Nazornost,vysvetleni
Názornost.
Nelze porovnávat třídy, žíky - každý potřebuje něco jiného. Ne direktivně
není to metoda pro každé dítě
Obě srovnatelné. Vždy záleží na učiteli.
Podle mě nezáleží na metodě, ale na učiteli. I v klasické matematice lze zkoumat a objevovat.
Podle mne je srozumitelnější 9 - 5 = 4, než pes = 2x husy
Pochopitelnější je naučení se jednoduchých postupů (zažití sčítání a odčítání do 20), poté můžeme přidat matematická prostředí, která děti rozvinou více. Nelíbí se mi, že v H-mat se počítá do 10 a najednou je vše i s přechodem, dopočítávání přes desítku. Slabší děti nemají moc šanci pochopit. Nyní zmiňuji pouze první třídu, našla bych více podnětů ke každému ročníku.
Pomocí prostředí si nenásilnou formou osvojuji základní matematické postupy. Je to hra, která je baví.
Praktické použití výpočtů.
Praktické příklady, které vidí, osahávají si, prožívají...
Predstavivost a porozumění
Pro každého něco jiného. Každý se najde v jiném prostředí.
Přijdou si na spoustu věcí samy
Přirozené objevování matematických zákonitostí, aniž by to tušily.
Rozklady čísel, jistota v základních matematických operacích, rozbor slovní úlohy.
Řekla bych, že systém úloh, způsob jejich řešení, některé děti nevidí důvod proč počítat sloupečky příkladů, je to pro ně nudné a nezazivne, pochopitelnejsi je pro ně celá matematika v podstatě.
Sami si prijdou na postup i reseni, vysvetluji,argumentuji a lepe si zapamatuji pravidla jak se ktere priklady pocitaji, jednotlive ulohy graduji takze maji dostatek casu pochopit zaklad
Učení je hlavně názornější, krásné učebnice a spousta pomůcek pro zkoumání.
V klasické matematice si děti osvojí zažité algoritmy, které opakováním zautomatizují. Pokud je jednou pochopí a procvičí, mohou zpravidla úspěšně v matematice fungovat. Vím o žácích, kteří v hodinách matematiky vedených h. metodou zastávali funkci pozorovatelů a v praxi měli problém např. s převáděním jednotek apod.
V začátcích (1. třída) je to pro ně hravé, ale hravá může být i klasická matematika.
Vse? Kdyz si mohou samy najit cestu, ktera je pro ne nejvhodnejsi, uchopit ulohy po svem, zakomponovat si je do sveho sveta.
Vše je názorné, že na to přicházejí samy. Pokud ne, vysvětlí spolužák, kterého lépe poslouchají.
Vysvětlování na nějakých příkladech. Samy na postup rozhodně většina není schopna přijít.
zásady Hejného matematiky (klima výuky, přiměřené možnosti pro každého žáka, získávání poznatků vlastní úvahou, komunikace mezi žáky navzájem a mezi žáky a učitelem, využivání teorie generického modelu); myšlenka, že matematika nejsou stohy sloupečků a slovních úloh o jablkách a hruškách
že se všechno děje postupně, obtížnost narůstá, nové věci se objevují logicky, v návaznosti na zkušenost dětí, ne ve stylu- dneska si probereme to a to, vede je ke spolupráci a umí si to vysvětlit společně mezi sebou
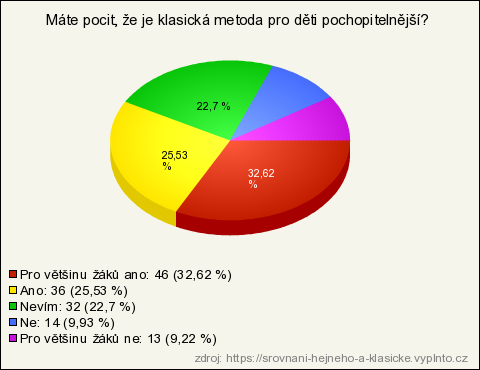
13. Máte pocit, že je klasická metoda pro děti pochopitelnější?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Pro většinu žáků ano | 46 | 32,62 % | 32,62 % |
| Ano | 36 | 25,53 % | 25,53 % |
| Nevím | 32 | 22,7 % | 22,7 % |
| Ne | 14 | 9,93 % | 9,93 % |
| Pro většinu žáků ne | 13 | 9,22 % | 9,22 % |
14. 14. Pokud ano, prosím uveďte, co je pro ně pochopitelnější.
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
a
Algoritmus úloh chápou i méně nadané děti.
dává jim osnovu, jak písemné dělit, násobit - jako kuchařka
Dostanou návod, vysvětlení
DOSTANOU UKÁZKU POSTUPU. I VELCÍ RÁDI VIDÍ - JAK TO DĚLAT A PKJ SE ZDOKONALÍ
Hejného?
Jasná struktura a postup práce. Až zažijí základy a naučí se je, mohou se dále rozvíjet v H-mat.
Jasně dané počty, násobilka zpaměti, ....
Jasné postupy
je jasně daný algoritmus- části dětí to vyhovuje, ale nepřipraví pro život
Je víc mechanická a méně na přemýšlení. Úlohy bývají jednodušší a všichni žáci mají možnost je pochopit.
Jednotnost pro vsechny deti
Již jsem uvedla. Cyklí se otázka.
Klasická metoda je srozumitelnější.
Klasickou metodu jsem neucila, rekla bych, ze pochopitelná pro děti bude taky, ale rozhodne nebude tak zajímavá a děti tolik nerozvíjí.
kombinuji s tvořivou školou a děti mají skvělé výsledky a matematiku mají rády, jak to tvrdí v Hejného metodě,
méně logicky uvažující děti se naučí počítat alespoň mechanicky
Mnoho dětí neumí uvažovat logicky a klasickou metodou se naučí počítat každé dítě.
Nabízí, jak můžou počítat některé typy úloh. Většina dětí není schopna bez návodu přijít, jak co počítat.
Neznám Hejného, nemohu srovnávat
numerace
Podle mě nezáleží na metodě, ale na učiteli. I v klasické matematice lze zkoumat a objevovat.
Pokud si jednou osvojí nějaký postup, nedělá jim ani v praxi problém ho používat.
Pro většinu žáků je logičtější Jde ověřit
propracovaná metodika založená na dlouhodobé praxi; mechanické výpočty zrychlují počítání
Prostě klasický dril je pochopitelný pro každého....skoro....
Příklady , kde není třeba logického myšlení.
Přímé, jednoznačné vysvětlení
System
Špatně položená otázka - něco pochopitelnější je, něco je v této metodě o naučení zpaměti - vzorce výpočtů ve vyšších ročnících - odvodit, ale pak musí znát
Už jsem uváděla.
Už ve školce se setkávají s klasickou matematikou, pokud mají staršího sourozence, většinou jej chtějí dohnat a proto nemívají větší obtíže při nástupu do školy.
V
ve všem, zvládnou ji všechny děti
vše
vše
Vše
Vše je jasné dané - rozklad při sčítání a odčítání, řady násobků, pravidla, stereotyp, nemůžou nic pokazit, pokud nespletou příklad. Některé věci se musí naučit zpaměti, přes to vlak nejede. U Hejného se vše objevuje, děti si objeví, ale druhou hodinu si už nepamatují, co že to objevily.
vše, je to lepší
Výklad
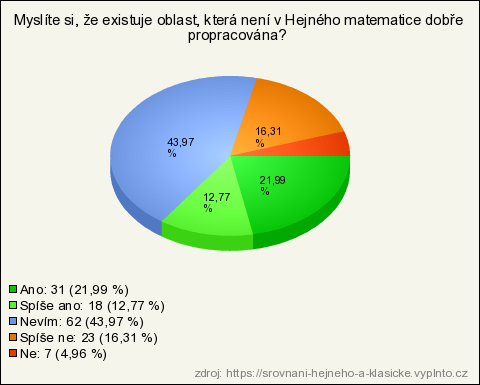
15. Myslíte si, že existuje oblast, která není v Hejného matematice dobře propracována?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Nevím | 62 | 43,97 % | 43,97 % |
| Ano | 31 | 21,99 % | 21,99 % |
| Spíše ne | 23 | 16,31 % | 16,31 % |
| Spíše ano | 18 | 12,77 % | 12,77 % |
| Ne | 7 | 4,96 % | 4,96 % |
16. Pokud ano, prosím uveďte jaká.
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
- indické násobení - Děda Lesoň - přepočítávání AG-EG-GG ...
a
Automatizace pocetnich spoju
binární soustava, "krokování"
Celá Hejného matematika.
Geometrické učivo
Geometrie - rýsování
Geometrie komplet. Pamětné počty, počítání se zlomky, desetinná čísla.
Geometrie- rýsování
geometrie, převody jednotek
geometrie, slovní úlohy
Geometrie.Přechod přes desítku.
Hejný mě hodně zajímal před lety, praxí jsem došla k názoru, že není samospasitelný a pro všechny
Hodnocení
Je zde menší prostor pro geometrii, rýsování.
Kalkulativni spoje
krok po kroku rozpracováno
Možná málo geometrie.
Možná taková ta "klasická" výuka - postupy atd. Mohou mít pak problém s přechodem na 2. stupeň, kde ty postupy vyžadují.
Myslím, že geometrie by mohla být propracovanější...
Násobilka
Násobilka - nelze ve třetí třídě stále hledat v tabulce.
násobilka, pamětné počítání, písemné počítání, geometrie
Nechápu, že někdo může říct, že děti nemusí počítat hbitě. A že si nemusí ani spočítat, kolik je bude stát nákup, protože platí kartou (to jsem slyšela od paní lektorky na vlastní uši). Dále se mi nelíbí, že ve třídě pracuje jen ten, kdo má zrovna dneska náladu a koho baví početní úkoly na dané téma.
Počítání s čísly většími než 1000 - najednou se v učebnici objeví, ale není tam popsaný rozvoj čísla v desítkové soustavě, chybí číselné řády, některé děti mají problém větší čísla vůbec přečíst.
Procvicovani
procvičování probraného
První ročník - přechod desítky, vyšší ročníky např. v geometrii není nikde nic a najednou mají děti přijít na povrch válce (3. ročník, tuším).
Převádění jednotek, dělení se zbytkem, dělení víceciferným dělitelem apod. Vím, že dnes jsou na to kalkulačky, ale je třeba to také umět.
Přijde mi, že na sebe učivo v první třídě tolik nenavazuje, počítá se s číslicemi, které se děti učí psát až třeba o pár týdnů později.
Sčítání s přechodem přes desitku.
T
téměř vše
téměř všechny, mino představivosti
učila jsem HM pouze 1. a 2. ročník, ve vyšších nemohu soudit
Upevnění zjištěného poznatku.
většina
vše
Vše
vše pamětné, násobilka, písemné počítání
všechny
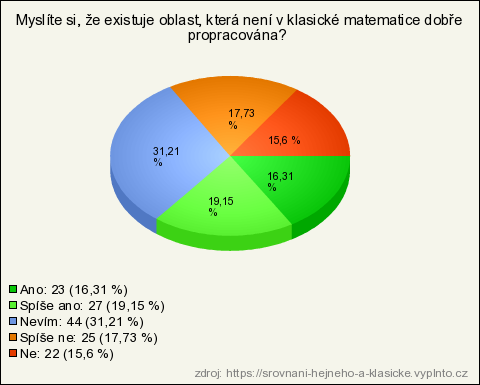
17. Myslíte si, že existuje oblast, která není v klasické matematice dobře propracována?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Nevím | 44 | 31,21 % | 31,21 % |
| Spíše ano | 27 | 19,15 % | 19,15 % |
| Spíše ne | 25 | 17,73 % | 17,73 % |
| Ano | 23 | 16,31 % | 16,31 % |
| Ne | 22 | 15,6 % | 15,6 % |
18. Pokud ano, uveďte prosím jaká.
Nepovinná otázka, respondent mohl napsat odpověď vlastními slovy.
-rozhodně geometrie
a
C
Celá geometrie.
Cvičení logiky, kombinatoriky, vědomí, že může existovat více řešení a více cest k řešení problému.
finanční gramotnost, práce s motivujícími texty
geometrie
Geometrie - rozvoj prostorové orientace
geometrie a prostorová představivost, kombinatorika,
Geometrie v rovině i v prostoru, násobilka
Logické myšlení
Logické myšlení a kombinace
Logické myšlení, samostatné hledání cest řešení.
logické úlohy
logické úlohy, kombinatorika, více řešení u příkladů
Logicke uloky
Logika
Logika
Málo úloh je zaměřeno na logické uvažování, na rozvoj matematické kreativity, vymýšlení neotřelých řešení.
Memorování učiva, kterému žáci nerozumí
Například řešení slovních a logických úloh...
Násobilka, prima nepřímá úměrnost, obvody a obsahy těles
Nelíbí se mi učebnice. Ve všech je hlavní prostor věnován na numeraci - sloupečky
Postup učení při násobilce od násobků 1 do 10
Práce s chybou, schopnost předat poznatek dalším, snadná objevit řešení.
procvičování učiva různými zajímavými úlohami
Prostor pro diskuzi, objevování, učení se manipulativy.
Představivost, názornost
Příklady, kde je třeba použít více názoru a didaktických pomůcek a nejsou k dispozici, tedy nejsou známy.
ŘEŠENÍ ÚKOLŮ JEN S MOŽNOSTÍ PSÁT VÝSLEDKY, POSTUPOVAT ÚSPĚŠNĚJEN NÁČRTKEM A VLASTNÍ CESTOU, ŘEŠENÍ VĚTŠINY ÚKOLŮ TYPU KLOKAN
slovní úlohy,geometrie
Slovní úlohy.
současné učebnice pro 1. stupeň nerespektují aktuální poznatky pedagogiky, psychologie a didaktiky
umět najít více řešení
Vsechny. Casto se nabizi malo (nekdy pouze jeden) postupu a vysvetleni.
všechny
Záleží na učebnici.
Zlomky.
Žádná
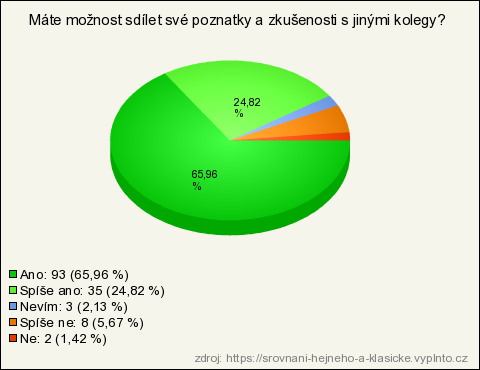
19. Máte možnost sdílet své poznatky a zkušenosti s jinými kolegy?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Ano | 93 | 65,96 % | 65,96 % |
| Spíše ano | 35 | 24,82 % | 24,82 % |
| Spíše ne | 8 | 5,67 % | 5,67 % |
| Nevím | 3 | 2,13 % | 2,13 % |
| Ne | 2 | 1,42 % | 1,42 % |
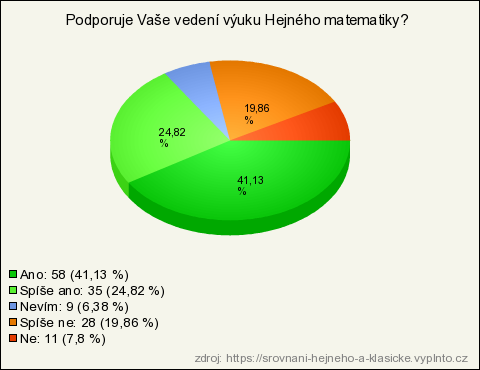
20. Podporuje Vaše vedení výuku Hejného matematiky?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Ano | 58 | 41,13 % | 41,13 % |
| Spíše ano | 35 | 24,82 % | 24,82 % |
| Spíše ne | 28 | 19,86 % | 19,86 % |
| Ne | 11 | 7,8 % | 7,8 % |
| Nevím | 9 | 6,38 % | 6,38 % |
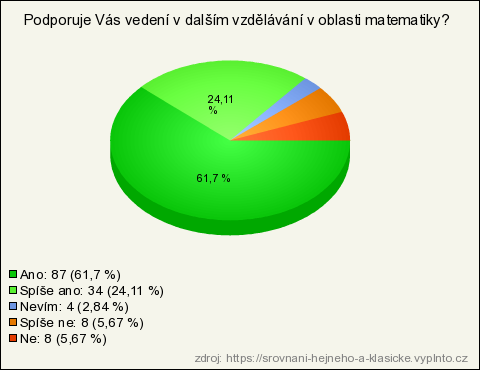
21. Podporuje Vás vedení v dalším vzdělávání v oblasti matematiky?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Ano | 87 | 61,7 % | 61,7 % |
| Spíše ano | 34 | 24,11 % | 24,11 % |
| Ne | 8 | 5,67 % | 5,67 % |
| Spíše ne | 8 | 5,67 % | 5,67 % |
| Nevím | 4 | 2,84 % | 2,84 % |
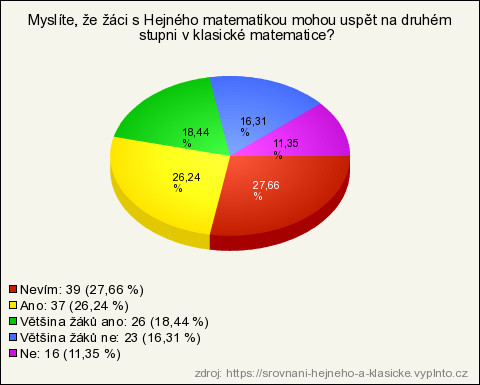
22. Myslíte, že žáci s Hejného matematikou mohou uspět na druhém stupni v klasické matematice?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Nevím | 39 | 27,66 % | 27,66 % |
| Ano | 37 | 26,24 % | 26,24 % |
| Většina žáků ano | 26 | 18,44 % | 18,44 % |
| Většina žáků ne | 23 | 16,31 % | 16,31 % |
| Ne | 16 | 11,35 % | 11,35 % |
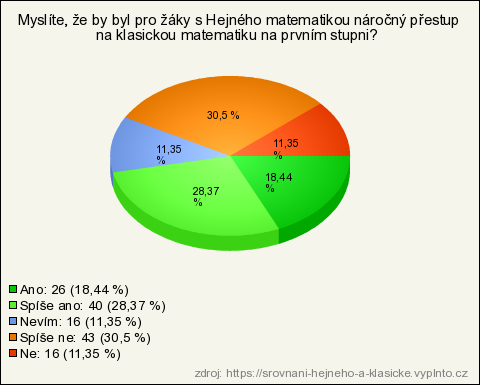
23. Myslíte, že by byl pro žáky s Hejného matematikou náročný přestup na klasickou matematiku na prvním stupni?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Spíše ne | 43 | 30,5 % | 30,5 % |
| Spíše ano | 40 | 28,37 % | 28,37 % |
| Ano | 26 | 18,44 % | 18,44 % |
| Ne | 16 | 11,35 % | 11,35 % |
| Nevím | 16 | 11,35 % | 11,35 % |
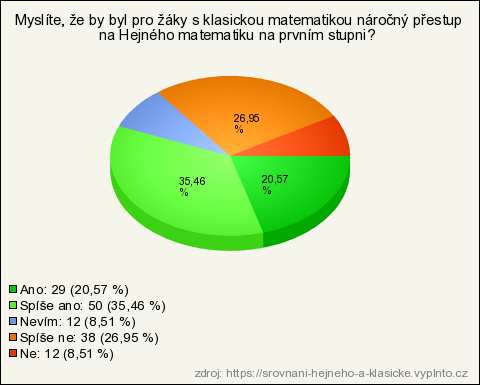
24. Myslíte, že by byl pro žáky s klasickou matematikou náročný přestup na Hejného matematiku na prvním stupni?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Spíše ano | 50 | 35,46 % | 35,46 % |
| Spíše ne | 38 | 26,95 % | 26,95 % |
| Ano | 29 | 20,57 % | 20,57 % |
| Nevím | 12 | 8,51 % | 8,51 % |
| Ne | 12 | 8,51 % | 8,51 % |
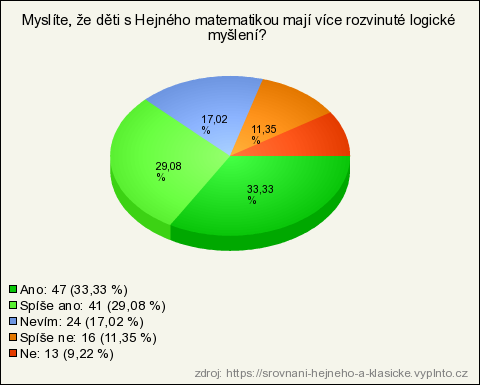
25. Myslíte, že děti s Hejného matematikou mají více rozvinuté logické myšlení?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Ano | 47 | 33,33 % | 33,33 % |
| Spíše ano | 41 | 29,08 % | 29,08 % |
| Nevím | 24 | 17,02 % | 17,02 % |
| Spíše ne | 16 | 11,35 % | 11,35 % |
| Ne | 13 | 9,22 % | 9,22 % |
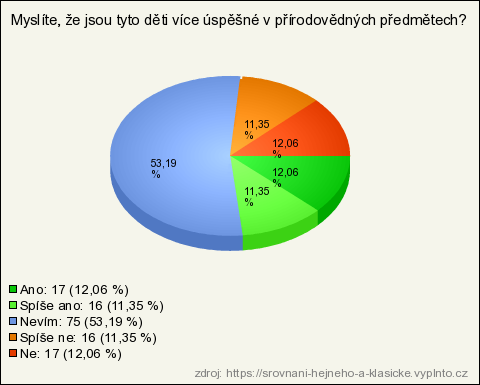
26. Myslíte, že jsou tyto děti více úspěšné v přírodovědných předmětech?
Povinná otázka, respondent musel zvolit jednu z nabízených odpovědí.
| Odpověď | Počet | Lokálně % | Globálně % |
|---|---|---|---|
| Nevím | 75 | 53,19 % | 53,19 % |
| Ano | 17 | 12,06 % | 12,06 % |
| Ne | 17 | 12,06 % | 12,06 % |
| Spíše ano | 16 | 11,35 % | 11,35 % |
| Spíše ne | 16 | 11,35 % | 11,35 % |
Citace
 Výsledky průzkumu podléhají licenci Creative Commons Uveďte autora 3.0 Česko
Výsledky průzkumu podléhají licenci Creative Commons Uveďte autora 3.0 Česko
Poznámky:
1) Globální procenta se počítají s ohledem na celkový počet respondentů, lokální četnost bere potaz pouze respondenty, kteří danou otázku zodpověděli.
2) U otázek typu "seznam - alespoň jedna" si mohli respondenti zvolit více odpovědí, proto součet procent u jednotlivých odpovědí nemusí dát dohromady 100 %
3) Na povinnou otázku musí respondent zodpovědět pouze v případě, kdy mu je zobrazena. Dotazník může obsahovat skoky mezi otázkami, takže lze na základě určitých odpovědí některé otázky přeskakovat.
4) Tato funkce je zatím v testovacím stadiu a je určena spíše pro zábavu - mějte na paměti, že může zobrazovat i nesmysly. V tomto momentě probíhá pouze automatická analýza dvojic výroků, zavislosti kombinací výroků můžete zatím sledovat pouze prostřednictvím funkce zjišťování závislostí odpovědí.


